贪心

2019-11-07

分治法

分治法的基本思想

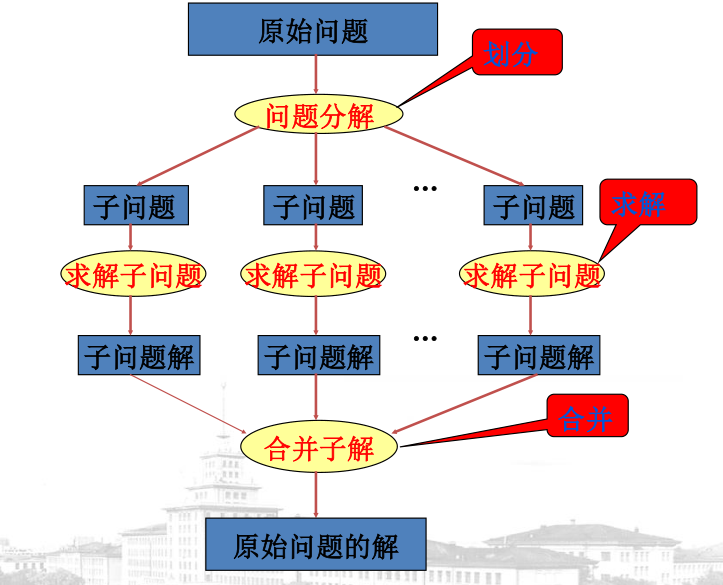
分治法的基本思想是将一个大规模的问题划分为若干个小规模的子问题，这些子问题相互独立且与原问题相同。递归的解决这些子问题，然后将各个子问题的解合并得到原问题的解。

而根据分治法的分割原则，应该把原问题分成多少个子问题才合适呢？没个子问题是否规模相等或怎样才最适当？通过大量实践发现，最好使子问题的规模大致相同，即将问题划分为大小相等的k个子问题比较合适。

二分搜索法

二分搜索是分治思想的典型例子

二分搜索（英语：binary search），也称折半搜索（英语：half-interval search）、对数搜索（英语：logarithmic search），是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

//while循环的方法
int BinarySearch(int a[],int n,int x){      //n为元素个数，k为搜索的数
	int left = 0；
	int right = n-1；
	while (left <= right){
		int middle = (left + right)/2;
		if (x == a[middle])
			return middle;
		else if (x>middle)
			left = middle + 1;
		else
			right = middle - 1;
	}

	return -1;
}
//递归的方法(java实现)
public static int BinSreachOfRecursion(int[] arr, int start, int end,int key) { 
	//start开始 end结束
		if(arr == null) {
			return -1;
		}
		//这个判断，必不可少，因为它就是递归种植的条件呀~
		if(start > end) {
			return -1;
		}
		int mid = (end - start)/2 + start;
		if(arr[mid] > key){
			return BinSreachOfRecursion(arr, start, mid-1, key);
		} else if(arr[mid] < key) {
			return BinSreachOfRecursion(arr, mid+1, end, key);
		} else {
			return mid;
		}		
	}

大整数乘法

大整数相乘：A、B两个整数，A有n位（123456……n），B有m位（123456……m），一般的思路是像最初学习乘法时一样逐位相乘后相加，但是这样做算法的复杂度过高，但这仍然是解题的基本思想。

既然提到分治，那么如何分，怎么治？下面参考如下

https://blog.csdn.net/qq_36165148/article/details/81132525

代码如下：

string multi(string A, string B) {
    int len_A = A.length();
    int len_B = B.length();
    if (len_A == 1) {
        if (len_B == 1) { 
        //最基本的情况：A和B都是一位数，把A、B从string转为int（我这里用的stringstream），然后相转string型return回去。
            ss << A;
            int a;
            ss >> a;
            ss.clear();
            ss << B;
            int b;
            ss >> b;
            ss.clear();
            ss << b*a;
            string str_out;
            ss >> str_out;
            ss.clear();
            return str_out;
        }
        else {  //A是个位数，B不是的情况下，按照分治的思想把B分开分别与A相乘。
            string B1, B2;
            B1 = B.substr(0, len_B / 2);
            B2 = B.substr(len_B / 2);
            string AB1 = multi(A, B1);
            string AB2 = multi(A, B2);
            if (AB2.length() > B2.length()) {
                string str = AB2.substr(0, 1);
                ss << str;
                int ab2;
                ss >> ab2;
                ss.clear();
                ss << AB1;
                int ab1;
                ss >> ab1;
                ss.clear();
                ss << ab1 + ab2;
                ss >> AB1;
                ss.clear();
                return AB1 + AB2.substr(1);
            }
            else
                return AB1 + AB2;
        }
    }
    else {
        if (len_B == 1) {  //B是个位数，A不是的情况与上述A是个位数B不是的情况相同。
            string A1, A2;
            A1 = A.substr(0, len_A / 2);
            A2 = A.substr(len_A / 2);
            string A1B = multi(A1, B);
            string A2B = multi(A2, B);
            if (A2B.length() > A2.length()) {
                string str = A2B.substr(0, 1);
                ss << str;
                int a2b;
                ss >> a2b;
                ss.clear();
                ss << A1B;
                int a1b;
                ss >> a1b;
                ss.clear();
                ss << a1b + a2b;
                ss >> A1B;
                ss.clear();
                return A1B + A2B.substr(1);
            }
            else {
                return A1B + A2B;
            }
        }
        else {  //A和B都不是个位数，就按照上述方法分治就可以了，只是为了最后相加的时候方便，把返回的四个部分都用0凑成了位数相同的。
            string A1, A2, B1, B2;
            A1 = A.substr(0, len_A / 2);
            A2 = A.substr(len_A / 2);
            B1 = B.substr(0, len_B / 2);
            B2 = B.substr(len_B / 2);
            string part1_ = multi(A1, B1);
            string part1_0(A2.length()+B2.length(), '0');
            part1_ = part1_ + part1_0;
            string part2_ = multi(A2, B2);
            string part2_00(part1_.length() - part2_.length(), '0');
            part2_ = part2_00 + part2_;
            string part3_ = multi(A1, B2);
            string part3_0(A2.length(), '0');
            part3_ = part3_ + part3_0;
            string part3_00(part1_.length() - part3_.length(), '0');
            part3_ = part3_00 + part3_;
            string part4_ = multi(A2, B1);
            string part4_0(B2.length(), '0');
            part4_ = part4_ + part4_0;
            string part4_00(part1_.length() - part4_.length(), '0');
            part4_ = part4_00 + part4_;
            return Plus(part1_, part2_, part3_, part4_);
        }
    }
}

原文链接：https://blog.csdn.net/qq_36165148/article/details/81132525

我还发现一种很有趣的解法大家可以看看：https://blog.csdn.net/tjsinor2008/article/details/5625849